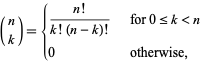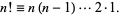On Being Joyful By Contract

"How joyful am I made by this contract!"

-- Shakespeare, Henry VI Part I
Act III, Scene I, Line 144

I can think of no book that has had more impact on my career than The Pragmatic Programmer by Dave Thomas and Andy Hunt.  One of the tips in The Pragmatic Programmer that I sadly do not find myself using a lot is Design with Contracts.

Design with Contracts
Use contracts to document and verify that code does no more and no less than it claims to do.
-- Dave Thomas and Andrew Hunt, The Pragmatic Programmer

Clojure has pre: and post: assertion functions, let us look at an example of the pre: assertion function in a prime tester function.

We can easily see this is not the worlds greatest prime test function, but the point is to look at the pre: assertion function.

We see that in order to call this function we must have the following: 1) the argument used in the call must be a number (defined by number? as instance? Number) and 2) the argument used in the call must not be negative.  We see by the tests that if either pre: condition is broken an AssertionError is thrown.  Thus allowing us to assume in the body of the function that we have a number and that it is not negative.

If one designs with contracts then one can easily reason about a system since one knows what each part of the system can produce.

Always Bet on Math

"If we offend it is with our good will.
That you should think we come not to offend
But with good will. To show our simple skill,
That is the true beginning of our end."
-- Shakespeare, A Midsummer Night's Dream
Act V, Scene I, Lines 108-111

Last week at work we did Pascal's Triangle as part of our weekly Code Dojo.  We followed the animated image on the Wikipedia entry as our guide to the algorithm.



This worked OK and we were able to solve it fairly quickly with something similar to the C# entry on Rosetta Code.  Something like this:

        public static void CreateTriangle(int n) {
            if (n > 0) {
                for (int i = 0; i < n; i++) {
                    int c = 1;
                    Console.Write(" ".PadLeft(2 * (n - 1 - i)));
                    for (int k = 0; k <= i; k++) {
                        Console.Write("{0}", c.ToString().PadLeft(3));
                        c = c * (i - k) / (k + 1);
                    }
                    Console.WriteLine();
                }
            }
        }

This code works but it does not really give the reader of it any idea as to what the code is for.  In order for someone to be able to follow this code they would have to run the algorithm a few times (in their heads, on paper, ...) to prove to themselves that it actually works.

In Rich Hickey's talk, "Hammock Driven Development", he talks about taking time to think.  Which reminds me of a quote often misattributed to Einstein:

Some years ago the head of the Industrial Engineering Department of Yale University said, "If I had only one hour to solve a problem, I would spend up to two-thirds of that hour in attempting to define what the problem is."
-- Robert E. Finley and Henry R. Ziobro, The Manufacturing Man and His Job
as quoted by Garson O’Toole at http://quoteinvestigator.com/2014/05/22/solve/

Let us spend a few minutes looking into what the problem actually is.

If look further down in the Wikipedia entry we see the following.


taken from https://commons.wikimedia.org/wiki/File:PascalsTriangleCoefficient.svg

Awesome, Pascal's Triangle can be reduced to binomial coefficients!  Since it has been about 13 years since I got my degree in mathematics I'll need to look up how to use and solve a binomial coefficient.  Luckily MathWorld give use the following:

Great, now all we need to do is have a way to solve for factorials, which we can also find on MathWorld!

We are now all set to solve the problem.

Here is my solution in Clojure:


(I did this as part of my daily kata)

We see in the Clojure code that I TDDed my way into: first a function which will find factorials, then a function to solve for binomial coefficients, and finally I a function which will give Pascal's Triangle.  Solving the problem in this way gives us not only a readable solution which allows someone reading the code to follow the solution but now we have a function for factorials and one for binomial coefficients!

Do not misread this blog post I am not saying that the solution given in C# above is wrong or bad, but only that by spending time to research a problem can often given a much more rich solution to the problem.

As IBM would say, "Think".

taken from http://www-03.ibm.com/ibm/history/ibm100/images/icp/P496146V03975A59/us__en_us__ibm100__cult_think__think_sign__620x350.jpg

Memoize OR How to Trim Your Function Budget

"Roman, remember by your strength to rule

Earth’s peoples—for your arts are to be these:
To pacify, to impose the rule of law,
To spare the conquered, battle down the proud."
-- Virgil, Aeneid
Book 6, Lines 1151 - 1154

Problem Statement

Say you have an operation in a function that cost a lot, like reading from a database or launching a missile.  You would like to be able to call the function as often as you need to for your algorithm but you would like to only do the database read or missile launch once if the arguments have not changed.  This is what memoize is used for.

How Memoize Works

Returns a memoized version of a referentially transparent function. The memoized version of the function keeps a cache of the mapping from arguments to results and, when calls with the same arguments are repeated often, has higher performance at the expense of higher memory use.
-- Memoize's doc string in clojure/core.clj

In my own words (yeah, I think in pictures).

In the image above we see that we always check to see if the cache for the function has a result already for the arguments given.  If it does already contain the arguments then return that result.  If it does not already have a result for the given arguments then: calculate it, store the result in the cache, and return the result.

Examples

In the example above we see that we have a function with the side effect of printing the string "Calculating...", thus when the function is called it will print the string and then return the result (think read from database or launch missiles).  When we wrap the function with a memoize and see that on the second call to the function we do not have any side effects!

Fin

There you have it, you can freely read from your database or launch missiles in your function without worrying about the number of times you call said function with the same arguments.