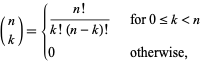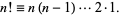Always Bet on Math

"If we offend it is with our good will.
That you should think we come not to offend
But with good will. To show our simple skill,
That is the true beginning of our end."
-- Shakespeare, A Midsummer Night's Dream
Act V, Scene I, Lines 108-111

Last week at work we did Pascal's Triangle as part of our weekly Code Dojo.  We followed the animated image on the Wikipedia entry as our guide to the algorithm.



This worked OK and we were able to solve it fairly quickly with something similar to the C# entry on Rosetta Code.  Something like this:

        public static void CreateTriangle(int n) {
            if (n > 0) {
                for (int i = 0; i < n; i++) {
                    int c = 1;
                    Console.Write(" ".PadLeft(2 * (n - 1 - i)));
                    for (int k = 0; k <= i; k++) {
                        Console.Write("{0}", c.ToString().PadLeft(3));
                        c = c * (i - k) / (k + 1);
                    }
                    Console.WriteLine();
                }
            }
        }

This code works but it does not really give the reader of it any idea as to what the code is for.  In order for someone to be able to follow this code they would have to run the algorithm a few times (in their heads, on paper, ...) to prove to themselves that it actually works.

In Rich Hickey's talk, "Hammock Driven Development", he talks about taking time to think.  Which reminds me of a quote often misattributed to Einstein:

Some years ago the head of the Industrial Engineering Department of Yale University said, "If I had only one hour to solve a problem, I would spend up to two-thirds of that hour in attempting to define what the problem is."
-- Robert E. Finley and Henry R. Ziobro, The Manufacturing Man and His Job
as quoted by Garson O’Toole at http://quoteinvestigator.com/2014/05/22/solve/

Let us spend a few minutes looking into what the problem actually is.

If look further down in the Wikipedia entry we see the following.


taken from https://commons.wikimedia.org/wiki/File:PascalsTriangleCoefficient.svg

Awesome, Pascal's Triangle can be reduced to binomial coefficients!  Since it has been about 13 years since I got my degree in mathematics I'll need to look up how to use and solve a binomial coefficient.  Luckily MathWorld give use the following:

Great, now all we need to do is have a way to solve for factorials, which we can also find on MathWorld!

We are now all set to solve the problem.

Here is my solution in Clojure:


(I did this as part of my daily kata)

We see in the Clojure code that I TDDed my way into: first a function which will find factorials, then a function to solve for binomial coefficients, and finally I a function which will give Pascal's Triangle.  Solving the problem in this way gives us not only a readable solution which allows someone reading the code to follow the solution but now we have a function for factorials and one for binomial coefficients!

Do not misread this blog post I am not saying that the solution given in C# above is wrong or bad, but only that by spending time to research a problem can often given a much more rich solution to the problem.

As IBM would say, "Think".

taken from http://www-03.ibm.com/ibm/history/ibm100/images/icp/P496146V03975A59/us__en_us__ibm100__cult_think__think_sign__620x350.jpg